归并排序

归并排序是一种经典的排序算法，它使用分治法的思想将一个大问题分解为多个小问题，然后将这些小问题的解合并起来得到最终的解。下面是对归并排序算法的自然语言描述：

1. 首先，将待排序的数组分成两个大致相等的子数组，这个过程称为分割（Divide）。
2. 对每个子数组递归地应用归并排序算法，将其进一步分割为更小的子数组，直到每个子数组只包含一个元素或为空为止。这个过程称为递归（Recursion）。
3. 当子数组无法再分割时，开始将它们合并（Merge）起来。合并的过程是将两个有序的子数组合并成一个有序的数组。
4. 重复步骤 3，直到所有的子数组都被合并成一个完整的、有序的数组。

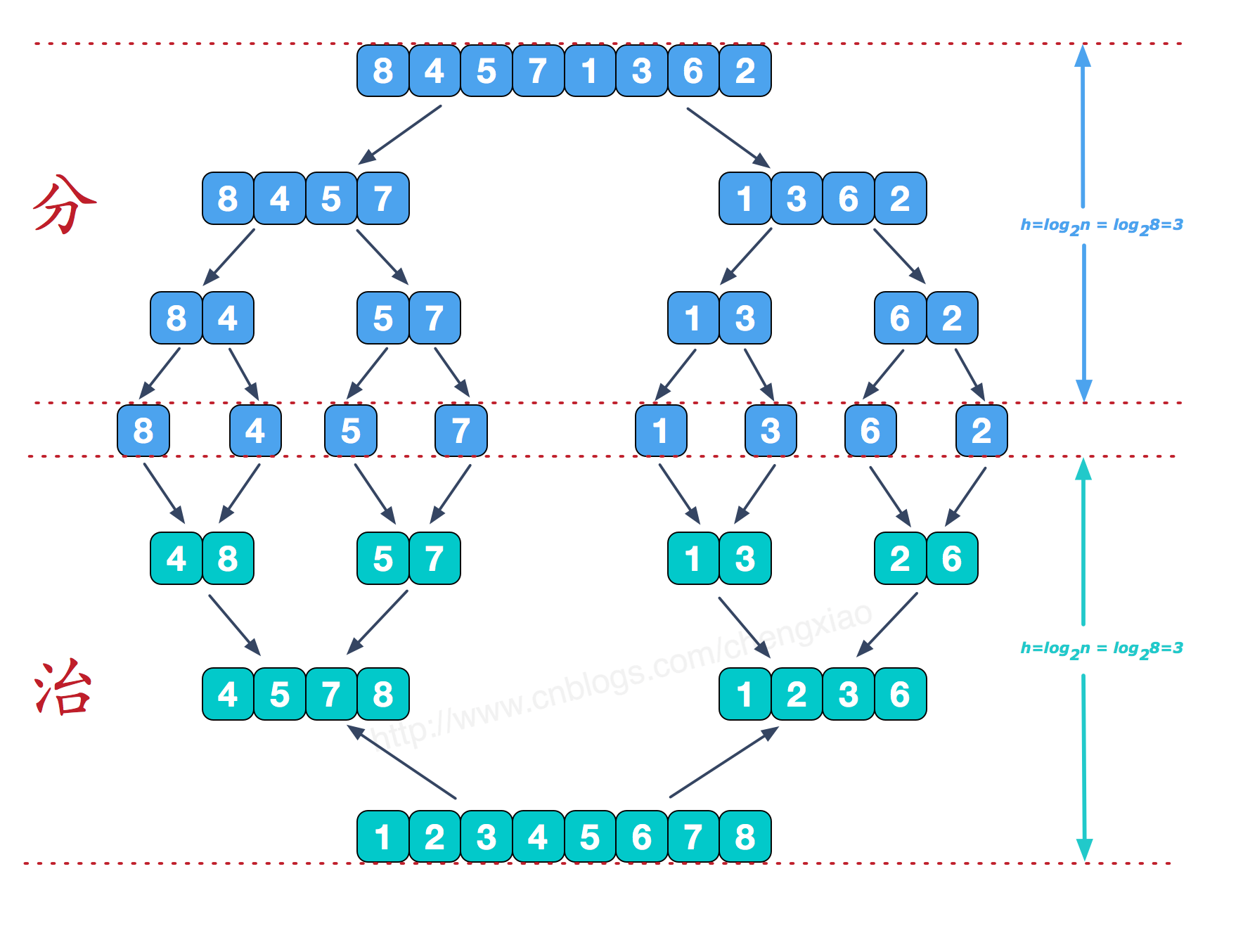
归并排序的关键在于合并过程。在合并过程中，我们需要比较两个子数组的元素。 由于子数组是有序的，所以子数组头部都是这个数组内最大（最小）的元素。然后合并时，将两个数组的头部的值取其中的最大（最小）值将它们依次放入新的数组中。 当其中一个子数组的元素已经全部放入新数组后，我们将另一个子数组中剩余的元素直接放入新数组的末尾。

归并排序的时间复杂度是 $O(nlogn)$，其中 $n$ 是待排序数组的长度。它是一种稳定的排序算法，适用于各种数据规模的排序任务。

#include <stdio.h>

// 合并两个有序数组
void merge(int arr[], int left[], int leftSize, int right[], int rightSize) {
    int i = 0, j = 0, k = 0;

    while (i < leftSize && j < rightSize) {
        if (left[i] <= right[j]) {
            arr[k++] = left[i++];
        } else {
            arr[k++] = right[j++];
        }
    }

    while (i < leftSize) {
        arr[k++] = left[i++];
    }

    while (j < rightSize) {
        arr[k++] = right[j++];
    }
}

// 归并排序
void mergeSort(int arr[], int size) {
    if (size <= 1) {
        return;
    }

    int mid = size / 2;
    int left[mid];
    int right[size - mid];

    // 将数组分成两部分
    for (int i = 0; i < mid; i++) {
        left[i] = arr[i];
    }

    for (int i = mid; i < size; i++) {
        right[i - mid] = arr[i];
    }

    // 递归地对左右两部分进行排序
    mergeSort(left, mid);
    mergeSort(right, size - mid);

    // 合并两个有序数组
    merge(arr, left, mid, right, size - mid);
}

// 打印数组元素
void printArray(int arr[], int size) {
    for (int i = 0; i < size; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    int arr[] = {9, 5, 2, 7, 1, 8, 3};
    int size = sizeof(arr) / sizeof(arr[0]);

    printf("原始数组：");
    printArray(arr, size);

    mergeSort(arr, size);

    printf("排序后数组：");
    printArray(arr, size);

    return 0;
}